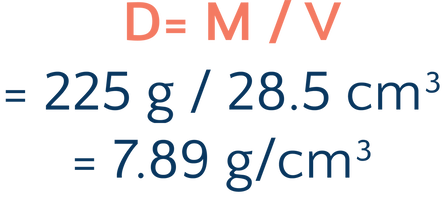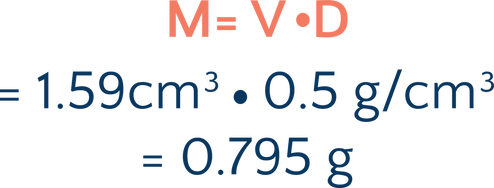Calculating Density
Calculating Density from a Given Mass and Volume
Now that you understand the concept of density, I do hope this next idea does not sound intimidating to you: we can actually use math to calculate the density of any given object.
Don’t worry, it’s pretty simple math. As you’ve learned, density goes down as volume goes up and density goes up as mass goes up. In other words, a marble that weighs one ounce will have a higher density than a beach ball that weighs one ounce, and a bowling ball of a particular size will have a higher density than a beach ball of the same size. From this basic conceptual understanding, we can derive an equation for density:
Don’t worry, it’s pretty simple math. As you’ve learned, density goes down as volume goes up and density goes up as mass goes up. In other words, a marble that weighs one ounce will have a higher density than a beach ball that weighs one ounce, and a bowling ball of a particular size will have a higher density than a beach ball of the same size. From this basic conceptual understanding, we can derive an equation for density:
D=M/V, where D is density, M is mass, and V is volume.
Try it out for yourself: what happens to D if M goes up, but V stays the same? What happens to D if V goes up, but M stays the same? Does this match your conceptual understanding of density?
Remember this equation. Know it like the back of your hand. There are a few mnemonics that might help you remember. One is “DMV,” which is where you go to get a driver’s license. Another is to just put “D equals M over V” to a catchy tune of your choosing. You will use this equation often, so it is important to know. If you forget, just remember that it relates back to everything you learned in the previous sublesson: density goes down as volume goes up and density goes up as mass goes up. D = M/V.
Fortunately, application of this equation is relatively simple—you just need to plug in the values for mass and volume, and presto, density! Now seems like an opportune time to mention that you can use a calculator whenever you want in this class. It’s still helpful to know how to do basic math without one, but we’ll leave that to your math teachers.
This video gives a helpful tutorial:
Try it out for yourself: what happens to D if M goes up, but V stays the same? What happens to D if V goes up, but M stays the same? Does this match your conceptual understanding of density?
Remember this equation. Know it like the back of your hand. There are a few mnemonics that might help you remember. One is “DMV,” which is where you go to get a driver’s license. Another is to just put “D equals M over V” to a catchy tune of your choosing. You will use this equation often, so it is important to know. If you forget, just remember that it relates back to everything you learned in the previous sublesson: density goes down as volume goes up and density goes up as mass goes up. D = M/V.
Fortunately, application of this equation is relatively simple—you just need to plug in the values for mass and volume, and presto, density! Now seems like an opportune time to mention that you can use a calculator whenever you want in this class. It’s still helpful to know how to do basic math without one, but we’ll leave that to your math teachers.
This video gives a helpful tutorial:
All substances--from atoms to galaxies--use the same formula for density.
Identifying Unknowns with the Density Equation
To understand why it is useful to know and be able to use this equation, consider a block of unknown origin. Let’s say it’s a perfect cube with an unfamiliar, apparently alien symbol on it that randomly crashed out of the sky one day:
Oooh, spooky...
We want to be able to figure out what it’s made of. One good way of doing this is to understand that density is a physical property of a substance, meaning that it won’t change based on the amount of that substance. It’s an inherent property of the substance. So, if two objects have exactly the same density, they are probably the same thing.
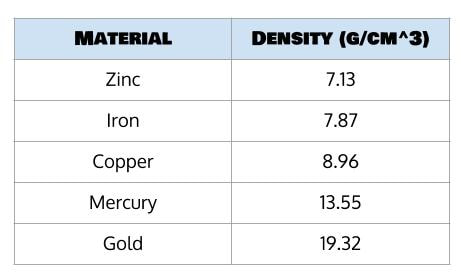
So let’s say that our block has a mass of 225 grams and a volume of 28.5 cm³. I know the usual density of these substances:
So let’s say that our block has a mass of 225 grams and a volume of 28.5 cm³. I know the usual density of these substances:
To solve this, we simply have to calculate the density of the block and compare it to the density of our known substances:
Factoring in just a little bit of rounding or measurement error, we can see that this is awfully close to the density of iron, which is 7.87 g/cm³. So, we still may not know why this mysterious cube fell out of the sky one day, but at least we know it’s made of iron. And isn’t there something comforting in knowing that something so unfamiliar is made of a very familiar element?
Rearranging the Equation
As with all equations, and Harry Styles, this equation doesn’t just work well in one direction. Let’s try working backwards with the equation.
Let’s imagine that, now that the scientists in charge of the mysterious space cube know that it’s made of iron, they’re able to cut through it. Inside, they find a mysterious glowy, floaty light orb thingy:
Let’s imagine that, now that the scientists in charge of the mysterious space cube know that it’s made of iron, they’re able to cut through it. Inside, they find a mysterious glowy, floaty light orb thingy:
Oooohhh, mystery. Because the ball is floaty, the scientists are not able to measure the mass directly. But, in order to do further experimentation and find out more about the object, they need to know the mass. They are able to measure the density by light scatter with a laser and measure the volume by fluid displacement in a special chamber. They determine that the volume is 1.59 cm3 and the density is 0.5 g/cm³—light as a feather! What is the mass of this object?
We can simply rearrange the formula for density to find out:
We can simply rearrange the formula for density to find out:
If you know any algebra, this rearrangement should make sense to you. If you don’t know algebra, you can use this handy triangle to help you out with the rearrangement:
So, calculating the mass of our mysterious orb:
Wow, super light! Knowing this, they’re able to do further experimentation that brings them closer to understanding the mysterious origins of their orb.
Summary
You should know:
- How to calculate density from a known mass and volume.
- How to calculate mass from a known density and volume.
- How to calculate volume from a known density and mass.
- How to identify an unknown material by calculating density and comparing it to a list of known densities.
Learning Activity
Content contributors: Emma Moulton and Emily Zhang